De cuantas formas se puede modularizar un sistema?
Este es un problema interesante, con unas cuantas consecuencias practicas.
Tengo una KB con n objetos y la quiero modularizar. Para simplificar, defino que quiero dividirla en K modulos, con 1<= k <= n.
De cuantas formas diferentes puedo modularizarla?
Sea S(n,k) la función que cuenta la cantidad de formas de modularizar, con n objetos y k modulos.
Dividimos el problema en 2 casos excluyentes:
Caso 1: Hago un modulo solo con el elemento n. Me quedan n-1 elementos, para agrupar en k-1 módulos, que puedo escribir de la forma S(n-1,k.-1).
Caso 2: n esta en un modulo con otros objetos. Esto es lo mismo que poner el objeto n en los k modulos que tienen los n-1 elementos restantes.
y puede escribirse como k * S(n-1,k)
La cantidad de forma de modularziar entonces, seria la suma de ambos casos y puede escribirse de la forma:
S(n,k) = S(n-1,k-1) + k* S(n-1,k)
a estos numeros se los conoce como números de Stirling de segunda especie.
La cantidad de formas de modularizar con n=7 y k = 4 es
S(7,4) = 7770
Algunos otros ejemplos:
S(50,6)= 1.1 * 10^36
S(10000,100)= 1.0 * 10^19842
El ultimo, es el que corresponde a tener una KB con 10.000 objetos y 100 módulos, que son cantidades parecidas a una KB que me toco modularizar hace poco. Ese numero es muy grande y explica porque es tan dificil modularizar kb grandes, pues el espacio de las soluciones factibles es enorme.
Para calibrar que tan grande es ese numero, las mejores estimaciones actuales dicen que la cantidad de atomos que hay en el universo conocido es del orden de 10^82,
Una KB con 100 objetos y 8 módulos, tiene muchas mas formas de modularizarse que los átomos del universo visible y el problema empeora mucho con la cantidad de objetos y módulos.
Tengo una KB con n objetos y la quiero modularizar. Para simplificar, defino que quiero dividirla en K modulos, con 1<= k <= n.
De cuantas formas diferentes puedo modularizarla?
Sea S(n,k) la función que cuenta la cantidad de formas de modularizar, con n objetos y k modulos.
Dividimos el problema en 2 casos excluyentes:
Caso 1: Hago un modulo solo con el elemento n. Me quedan n-1 elementos, para agrupar en k-1 módulos, que puedo escribir de la forma S(n-1,k.-1).
Caso 2: n esta en un modulo con otros objetos. Esto es lo mismo que poner el objeto n en los k modulos que tienen los n-1 elementos restantes.
La cantidad de forma de modularziar entonces, seria la suma de ambos casos y puede escribirse de la forma:
S(n,k) = S(n-1,k-1) + k* S(n-1,k)
a estos numeros se los conoce como números de Stirling de segunda especie.
La cantidad de formas de modularizar con n=7 y k = 4 es
S(7,4) = 7770
Algunos otros ejemplos:
S(50,6)= 1.1 * 10^36
S(100,80) = 5.0 x 10^85
S(1000,10)= 2.7 * 10^993S(10000,100)= 1.0 * 10^19842
El ultimo, es el que corresponde a tener una KB con 10.000 objetos y 100 módulos, que son cantidades parecidas a una KB que me toco modularizar hace poco. Ese numero es muy grande y explica porque es tan dificil modularizar kb grandes, pues el espacio de las soluciones factibles es enorme.
Para calibrar que tan grande es ese numero, las mejores estimaciones actuales dicen que la cantidad de atomos que hay en el universo conocido es del orden de 10^82,
Una KB con 100 objetos y 8 módulos, tiene muchas mas formas de modularizarse que los átomos del universo visible y el problema empeora mucho con la cantidad de objetos y módulos.
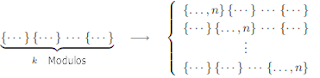


Comentarios
Publicar un comentario
1) Lee el post
2) Poné tu opinión sobre el mismo.
Todos los comentarios serán leidos y la mayoría son publicados.